The net magnetic field refers to the overall magnetic field resulting from the combination of multiple magnetic fields acting on an object or within a given region. It is essential in various scientific and engineering applications, such as electromagnetism, electrical devices, and magnetism-based technologies. This article aims to provide a detailed explanation of the net magnetic field and its significance.
Magnetic Fields and their Characteristics

To comprehend the concept of a net magnetic field, it is crucial to grasp some fundamental aspects related to magnetic fields. Here are key points to consider:
- Magnetic Field: A magnetic field is a region in space where a magnetic force can be experienced. It is produced by magnets, electric currents, or changing electric fields.
- Magnetic Field Strength: The strength of a magnetic field is determined by the intensity of the magnetic force it exerts on charged particles. It is typically measured in units of teslas (T) or gauss (G).
- Magnetic Field Lines: Magnetic field lines provide a visual representation of the direction and intensity of a magnetic field. They form closed loops and indicate the path a hypothetical north magnetic pole would follow when placed in the field.
Net Magnetic Field Calculation
Calculating the net magnetic field involves considering the superposition principle, which states that the total magnetic field at a point due to multiple sources is the vector sum of the individual magnetic fields at that point. Here’s how you can calculate the net magnetic field:
- Identify all the magnetic sources contributing to the net magnetic field.
- Determine the magnitude and direction of each magnetic field generated by these sources.
- Use vector addition to sum up the individual magnetic fields to obtain the net magnetic field.
In mathematical terms, the net magnetic field ((B_ = B_1 + B_2 + B_3 + \ldots]
where (B_1, B_2, B_3,) etc., represent the individual magnetic fields.
Factors Affecting the Net Magnetic Field
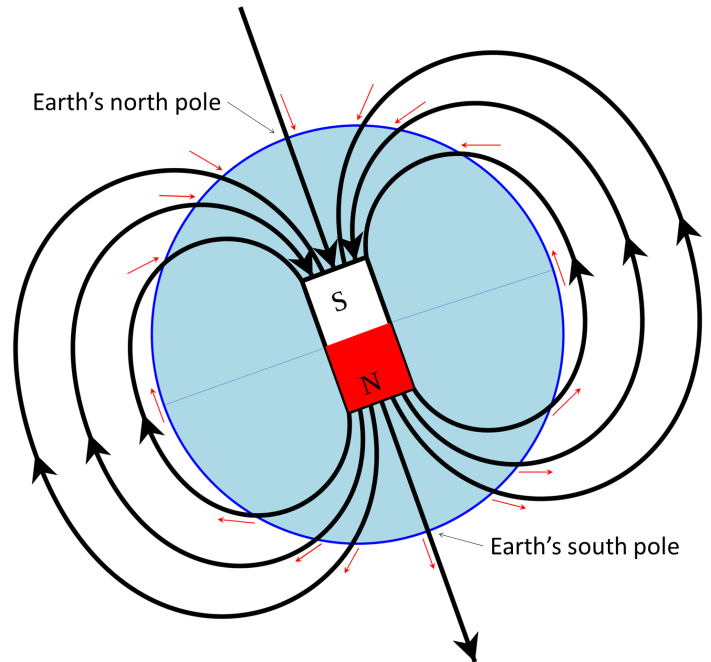
Several factors influence the net magnetic field’s strength and direction. Understanding these factors is crucial for predicting and manipulating magnetic fields. Here are some notable factors:
- Distance: As you move away from a magnetic source, the magnetic field strength decreases inversely with the square of the distance (inverse-square law).
- Orientation: The relative alignment between the magnetic field and the observer affects the perceived strength. The magnetic field is strongest when measured perpendicular to the direction of the field lines and weakest when measured parallel to them.
- Magnetic Materials: The presence of ferromagnetic or paramagnetic materials in the region can alter the net magnetic field. These materials can concentrate or redirect magnetic field lines.
- Current Flow: Electric currents generate magnetic fields. By controlling the current flow, either through straight wires or coils, the net magnetic field can be adjusted.
Applications of Net Magnetic Field

The net magnetic field finds applications in various domains, including:
- Electromagnetic Devices: Motors, generators, transformers, and solenoids rely on the net magnetic field to generate mechanical motion or induce electrical currents.
- Magnetic Resonance Imaging (MRI): In medical diagnostics, MRI machines utilize the net magnetic field to create detailed images of internal body structures by manipulating the alignment of atomic nuclei.
- Magnetic Data Storage: Hard drives and magnetic tapes use the net magnetic field to store and retrieve digital information encoded as magnetic patterns.
- Magnetic Levitation: Technologies like magnetic levitation trains (Maglev) employ the net magnetic field to suspend and propel trains using magnetic repulsion.
- Magnetometers: These instruments measure the intensity and direction of magnetic fields, aiding in geological surveys, navigation systems, and research applications.
The formula for the net magnetic field, denoted as Bnet, can be expressed as follows:
Bnet = B1 + B2 = 2RμI(1 + π1)
Let’s break down the formula step by step:
- B1 and B2 represent the individual magnetic fields produced by two separate sources or elements.
- The net magnetic field, Bnet, is obtained by adding the individual magnetic fields, B1 and B2. This accounts for the combined effect of both sources on a given point in space.
- The term “2RμI” represents a common factor that relates to the geometry and properties of the sources.
- R refers to the distance between the source and the point where the magnetic field is being measured. It represents the distance from the center of the source to the observation point.
- μ (mu) stands for the permeability of the medium in which the magnetic field is being measured. In most cases, the medium is air, and its permeability is approximately equal to the permeability of free space, represented as μ0.
- I denotes the current flowing through the sources. It represents the strength of the electric current passing through the wires or coils that generate the magnetic fields.The term “(1 + π1)” incorporates a correction factor that depends on the specific configuration of the sources.
- The π1 factor is given by the equation π1 = (r1^2 – R^2)/(r1^2 + R^2), where r1 represents the radius or characteristic length of the first source.
- This correction factor takes into account the relative distances between the sources and the observation point. It adjusts the magnetic field strength based on the geometry of the sources and their positions.
In summary, the net magnetic field formula Bnet = B1 + B2 = 2RμI(1 + π1) calculates the combined magnetic field strength at a specific point resulting from two separate sources. It considers the distances, currents, and geometries of the sources to provide an accurate representation of the net magnetic field.
Summary
In summary, the net magnetic field represents the combined effect of multiple magnetic fields on an object or within a given region. It is obtained through vector addition of individual magnetic fields. Factors such as distance, orientation, magnetic materials, and current flow influence the net magnetic field’s characteristics. Understanding the net magnetic field is crucial for a wide range of applications, including electromagnetism, medical imaging, data storage, transportation, and scientific measurements.


